머신러닝

Gradient Descent(경사하강법)

느린 개미 2023. 2. 9. 11:53
반응형

 

머신러닝 기반 회귀의 핵심 사항은 비용함수를 최소로 만드는 w1, w0 변수가 무엇인지 알아내는 것이다.

 (여기서는 단순선형 회귀라고 가정한다. y = w0  + w1 * x)

 

비용함수를 최소로 하는 w1, w0 가 무엇인지 찾아보는 방법이 경사하강법 이다.

실제 y 와 예측된 y_pred 의 차이를 계산하는 비용함수는 아래와 같다.

 

비용함수를 단순히 y=x^2 로 나타내보면 위의 그래프와 같은데, 여기서 두가지 사항을 눈여겨보자.

 

1) 방향성

기울기+ 인 경우 : x 값이 작아질수록 y 가 작아지고,

기울기-  인 경우 : x값이 커질수록 y 가 작아짐을 알 수 있다.

 

2) 크기

y (비용함수)가 작을 수록 : 기울기가 작아지고

y (비용함수)가 클수록 : 기울기가 커진다.

 

따라서, w1_update = w1 - 기울기(즉, 미분값) 의 개념으로 이해하면,

방향성과 크기 두가지 모두 반영된다고 할 수 있다.

 

기울기가 너무 클 수 있기에 보통 머신러닝 학습에서는 learning_rate(0.01, 0.001 등) 를 곱해준다. 

따라서 Gradient Descent 로 w1, w0 을 구하는 개괄적 개념은 아래 식으로 정리된다. 

 

w1_update = w1 - learning_rate *기울기(즉, w1 미분값)

w0_update = w0 - learning_rate *기울기(즉, w0 미분값)

 

그럼 이제 파이썬 코드로 확인해보도록 하겠다.

 위의 비용함수를 각각 w1, w0 로 편미분 하면 아래와 같다. 

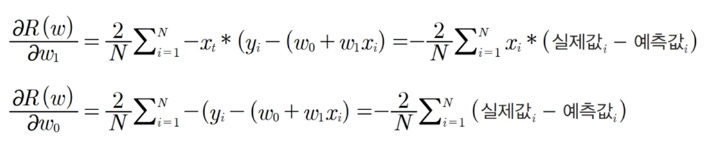
import matplotlib.pyplot as plt
import numpy as np

np.random.seed(0)
#y에 표준정규분포 추출 값을 더해주는 이유는 오차 생성을 위해서다.
X = 2*np.random.rand(100,1)
y = 6 + 4*X + np.random.randn(100,1)

plt.scatter(X,y)
#X,y 값에 대한 산점도는 아래와 같다. 오차가 최소가 되는 회귀식을 구해보자 h(x) = w1*X + w0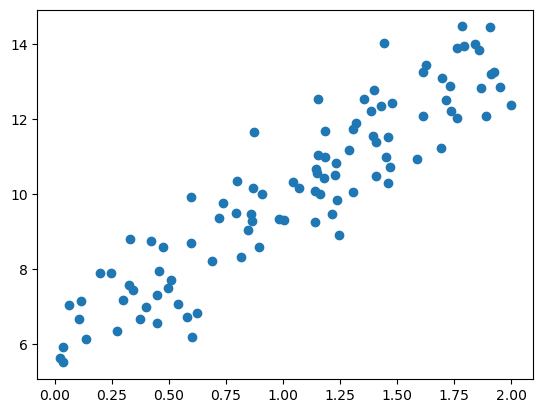

#비용함수 MSE
def get_cost(y, y_pred):
    
    N = len(y)
    cost =  np.sum(np.square((y-y_pred)))/N
    
    return cost
    
#비용함수를 w1, w0 로 미분하여 그 기울기만큼 빼주며 값을 업데이트 한다. 
def get_weight_updates(w1, w0, X, y, learning_rate = 0.01):
    N = len(y)
    
    #먼저 w1_update, w0_update를 각각 w1, w0 의 shape 과 동일한 크기를 가진 0값으로 초기화.
    
    w1_update = np.zeros_like(w1)
    w0_update = np.zeros_like(w0)
    
    y_pred = np.dot(X, w1.T) + w0
    diff = y-y_pred
    
    w0_factors = np.ones((N, 1))
    
    w1_update = -(2/len(y)) * learning_rate * np.dot(X.T, diff)
    w0_update = -(2/len(y)) * learning_rate * np.dot(w0_factors.T, diff)
    
    return w1_update, w0_update
    
def gradient_descent_steps(X, y, iters=10000):
    w0 = np.zeros((1,1))
    w1 = np.zeros((1,1))
    
    #인자로 주어진 iters 만큼 반복적으로 get_weight_updates()를 호출해 w0, w1 업데이트. 
    
    for ind in range(iters):
        w1_update, w0_update = get_weight_updates(w1, w0, X, y , learning_rate=0.01 )
    
        w1 = w1 - w1_update
        w0 = w0 - w0_update
    
    return w1, w0

실제 위의 함수를 수행한 결과로 얻은 w1, w0 결과는 아래와 같다.

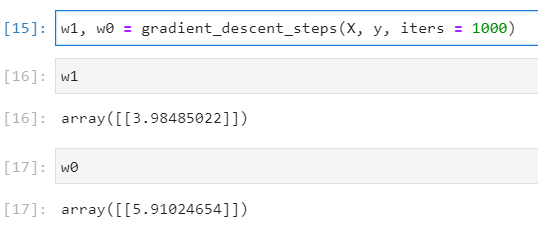
실제 값과 회귀식을 그래프로 표현하면 아래와 같다.

 

참고 사이트:

https://angeloyeo.github.io/2020/08/16/gradient_descent.html

https://velog.io/@gjtang/%ED%8C%8C%EC%9D%B4%EC%8D%AC-%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-%EC%99%84%EB%B2%BD-%EA%B0%80%EC%9D%B4%EB%93%9C-Section5

참고 도서, 코드 출처 : 파이썬 머신러닝 완벽가이드 

반응형